• Laser Fluence (Energy)
• Laser Fluence (Average Power)
• LIDT Scaling Law
• Photon Unit Converter
• Spot Size Scaling (Wavelength)
• Gaussian Spot Size (in Focus)
• Diffraction by Grating (Angle)
• Laser Damage Testing

 

Peak Fluence: ... J/cm²

Peak Power: ... MW/cm²

Laser – Induced Damage Threshold (LIDT) is a measure frequently reported in units of (peak) Fluence or (peak) Power Density. Let us take a closer look how it is evaluated. Laser fluence is a measure used to describe the optical energy delivered per unit (or effective) area. Within the community of laser scientists and technicians it is very common to describe fluence in units of J/cm². To calculate fluence use following formula:

For Gaussian beams effective focal spot area it is determined at I₀/e level of maximal intensity by CCDs and converted into the units of square centimeters. In case when I₀/e² or I₀/2 (FWHM) criteria is used additional factors have to be taken into account that are often forgotten. See figure for details.

Sometimes (in other communities) intensity or power density is used instead of fluence:

while the peak power is defined as

Peak fluence is by far one of the most important parameter that requires accurate characterization.

For angles of incidence differing from 0 degrees, the cosine of the angle has to be included in the calculation of the effective area. Therefore the enlargement of beam diameter due to arbitrary angle of incidence (AOI) must be taken into account when calculating fluence:

 

Peak Fluence: ... J/cm²

Peak Power: ... MW/cm²

Pulse Energy: ... mJ

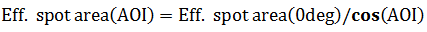
Laser – Induced Damage Threshold (LIDT) is a measure frequently reported in units of (peak) Fluence or (peak) Power Density. Let us take a closer look how it is evaluated. Laser fluence is a measure used to describe the optical energy delivered per unit (or effective) area. Within the community of laser scientists and technicians it is very common to describe fluence in units of J/cm². If the average power is used to characterize repetitive laser pulses then pulse energy should be calculated by dividing average power by repetition rate:

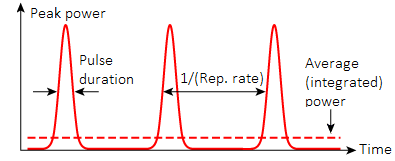
Then following formula is used to calculate laser peak fluence:

For Gaussian beams effective focal spot area it is determined at I₀/e level of maximal intensity by CCDs and converted into the units of square centimeters. In case when I₀/e² or I₀/2 (FWHM) criteria is used additional factors have to be taken into account that are often forgotten. See figure for details.

Sometimes (in other communities) intensity or power density is used instead of fluence:

while the peak power is defined as

Peak fluence is by far one of the most important parameter that requires accurate characterization.

For angles of incidence differing from 0 degrees, the cosine of the angle has to be included in the calculation of the effective area. Therefore the enlargement of beam diameter due to arbitrary angle of incidence (AOI) must be taken into account when calculating fluence:

 

LIDT: ... J/cm²

For pulse durations <20 ps this scaling law LIDT is not applicable. In this case LIDT of optics should be tested individually. Contact LIDARIS experts for more details.

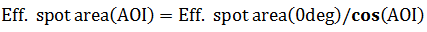
Optical damage mechanisms depend on laser pulse durations – τ [1]. However in the range between 10^-11 s and 10^-9 s 1-on-1 damage threshold fluence might be scaled by law: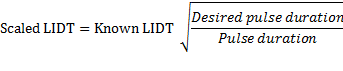

Within long-pulse regime (>20 ps up to ms) transfer of electron kinetic energy to the lattice and diffusion takes place during the laser pulse. The longer the pulse duration, the more energy the optic can handle. For short-pulse (< 20 ps) pulse duration law is no longer applicable. Optics should be tested individually. Also, for pulse durations in the range of ms, the CW LIDT must be checked.

 

Pulse width dependence of threshold damage fluence for fused silica. This graph was obtained from [1].

[1] B. C. Stuart et al., Phys. Rev. B, 53, 1749 (1996).

For quick conversions, enter a value into any of the boxes, and the remaining units will be calculated automatically. The inter-relations between different units are provided by formulas below:

 

1. In physics, the wavelength λ of the sinusoidal wave is the spatial period of the wave - the distance over which the wave's shape repeats.

 

2. in spectroscopy, the wavenumber v of electromagnetic radiation is defined as

 

3. The electron volt (eV) is a unit of energy equal to approximately 1.6×10−19 joule (J). The energy E and wavelength λ of a photon are related by

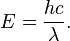
where h is the Planck constant, c is the speed of light.

 

Spot size in focus
at desired wavelength (1/e): ... μm

In case when the same lens is used for focusing of Gaussian beams at different wavelengths (in example laser harmonics) it is practical to know how much the beam diameter would change because of the wavelength. This calculator enables easy scaling of Gaussian beam focused by an aberration free lens with wavelength used in your measurement. Enter required data into the boxes to calculate spot size changes.

 

 

λ1 - actual wavelength: known wavelength of actual spot size in focus.

λ2 - desired wavelength: other wavelength that you desire to use with the same lens.

Dwaist1 - actual spot size in focus: spot size in focus at defined level of intensity.

 

Focused spot size diameter: ... μm

Rayleigh Range: ... mm

This calculator evaluates spot size of Gaussian beam focused by an aberration free lens. Enter required data into the boxes to calculate focused spot size diameter and Rayleigh range for your measurement. You might get to know required parameters by fallowing below provided tutorial.

 

1. Considering an optical system in air lens focal length is the distance over which initially collimated rays are brought to a focus. It is basic description of the lens and usually provided by the production. However, you should note that focus length of the same lens differs for different wavelengths.

2. In physics, the wavelength λ of the sinusoidal wave is the spatial period of the wave - the distance over which the wave's shape repeats.

3. M² is the beam quality factor. It provides a simple means for accurately calculating the most commonly required parameters of real world laser beams, namely, divergence angle, propagation characteristics over a distance, and the size of focused spots.

4. Spot size diameter (marked as DL in the figure) is the diameter of the beam spot size at the I₀/e² level of intensity on the entrance of the lens.

5. Focused spot size (marked as Dwaist in the figure) is the diameter of the focused spot size at the I₀/e² level of intensity. It is calculated as:

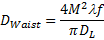
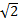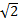6. Rayleigh range (marked as zR in the figure) is a very common and useful beam metric. It defines distance over which the beam diameter increases by a factor of , and its cross sectional area doubles. It is calculated as:

 

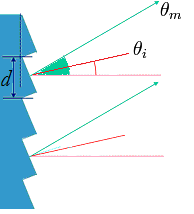
Diffraction Grating is an array of equally spaced lines that concentrate the light in a few directions determined by the spacing d (of the lines) and wavelength λ of the light. When light is incident on the diffraction grating at any arbitrary angle θi, the trasmitted or reflected light will deviate from its initial propagation dierction (zero-order mode, m=0), and have maxima at angles θm given by equation:

 

Higher order diffraction maxima m can be either positive or negative, thus resulting in diffracted light on both sides of the zero order beam.

We hope you have enjoyed Lidaris Calc. It was created in order to save your valuable time and prevent laser damage of your laser optics by considering laser fluence. In case you are still facing issues related to Laser-Induced Damage Threshold (LIDT) phenomena get one free consultancy from Lidaris experts.

Get in touch with LIDARIS: